Teoría I
Los sistemas matemáticos
de proporcionalidad surgidas del concepto pitagórico de que "todo es número"
de la creencia de que ciertas relaciones numéricas reflejan la estructura armónica
del universo, Una de estas relaciones, en vigencia desde la antigüedad hasta
nuestros días es la proporción conocida como sección áurea. Los griegos ya
descubrieron su importante cometido en la proporción del cuerpo humano. Al
creer que el hombre y los templos debían pertenecer a un orden universal más
elevado en la misma estructura de los templos se ponían de manifiestos estas
proporciones.
La sección áurea
merecieron también atención de los arquitectos del renacimiento. En tiempos más
recientes, Le Corbusier basó su sistema modular en la sección áurea, y su
aplicación en la arquitectura que perdura hoy en día. .
La sección áurea
puede definirse geométricamente como un segmento rectilíneo dividido de manera
que la parte menor es a la mayor como esta lo es a la total algebraicamente se
expresa mediante una ecuación de dos razones a/b=b/(a-b)
Las propiedades de que
goza explican su presencia en la arquitectura y en la estructura de los
organismos vivos, cualquier progresión que se base en la sección áurea será
al mismo tiempo a la aritmética y geométrica. En la progresión numérica Q1,
Q2, Q3,.. Qn cada elemento es la suma de dos
anteriores. Otra serie que se aproxima a la áurea es la serie numérica de
Fibonacci: 1,1,2,3,5,8,13 etc.
De nuevo cada número
es igual a los dos que le anteceden y la razón entre dos términos consecutivos
tiende a acercarse a la sección áurea conforme progresa la serie.
En
1497, un fraile italiano llamado Lucca Pacioli escribió un libro donde se reveló,
por fin, el secreto de la belleza. Se titula De divina Proportione, y su
tema central es lo que los escolares de nuestros días conocen como "regla
de tres". Pacioli se inspiraba en las ideas de Piero della Francesca, un
hombre que hoy conocemos a través de su obra pictórica, pero que en su tiempo
era más conocido por ser el autor de De Abaco, un manual de matemática
para comerciantes.
La
regla de tres era una herramienta básica para los comerciantes del Quattrocento:
servía para determinar las proporciones de capital, tierras, volumen de grano o
cualquier otra clase de bienes que le correspondía a cada socio, heredero o
copropietario ante un total determinado. Se la conocía entonces como regla
de oro o llave del comerciante.
La
educación de la época se centraba, luego del aprendizaje básico de la
lectoescritura, en las matemáticas, especialmente el cálculo de volúmenes (cuánto
grano hay en esa pñila, cuánto aceite hay en ese barril) y de las proporciones
(reparto de beneficios entre asociados).
Piero
della Francesca aplicaba en sus pinturas una serie de fórmulas que su público
estaba capacitado para comprender. Ese público estaba formado mayoritariamente
por comerciantes acaudalados que tenían la formación matemática necesaria
para percibir la belleza de la forma abstracta de un volumen cuya cuantía sabían
calcular mediante el cálculo.
Una
regla de tres famosa es la llamada Escala Armónica Pitagórica, que al modo
renacentista se expresa:
6
8 9 12
Según
nuestro estilo, la escribiríamos así:
6:8
= 9:12
Los
musulmanes la planteaban tal como en la escuela se enseña la regla de tres a
los niños:
6
------------- 8
9
------------- 12
Algunos
arquitectos relacionaron la escala armónica pitagórica, utilizada para
representar una escala musical, con el diseño visual modular o proporcional.
Andrea Palladio dejó asentada una falacia de diseño según la cual los
espacios pueden ser diseñados "musicalmente" de acuerdo con esta
escala: como el intervalo entre 6 y 12 es de una octava, entre 6 y 9 y entre 8 y
12 es de una quinta, entre 6 y 8 y entre 9 y 12 de cuarta y entre 8 y 9 de un
tono, si se organizaban las dimensiones de las habitaciones de un edificio
siguiendo esta serie, entonces se estaría produciendo una armonía espacial de
la misma clase que la que relaciona las notas musicales. La regla de oro
parecía una fórmula perfecta que relacionaba las artes de la música, la
pintura y la arquitectura. Y además mantenía las buenas relaciones
comerciales.
Cuando
Lucca Pacioli escribió La Divina Proporción, lo que hizo fue tomar otro
tipo de regla de tres, que, partiendo de una unidad arbitraria permitía la
construcción de proporcionalidades tanto de múltiplos como de submúltiplos
(intervalos mayores y menores). Los aficionados (en particular los fotógrafos,
grandes entusiastas) conocen esta relación como sección áurea. Su
expresión matemática es
a:b=b:a+b
Pacioli
decidió que esta relación era una expresión de armonía divina. Este cura había
educado a muchos hijos de ricos comerciantes, y sus libros sobre aritmética,
regla de tres y geometría fueron exitosos textos de estudio durante muchas décadas.
Sus ex alumnos, ahora clientes de arte, veían el mundo a través de sus ojos
matemáticos. Desde entonces, la sección áurea influyó bastante –aunque no
tanto como a veces se afirma- en la composición del encuadre en la pintura
occidental. Su difusión contemporánea se debe en gran medida a su adopción
axiomática por parte de Le Corbusier, a través de su método supuestamente
científico de componer, el Modulor.
Para
algunos, esta regla manifestaba un modo culturalmente programado de ver; para
otros, más inocentes o menos inquietos, la sección
áurea es una proporción natural, que puede encontrarse tanto en las
proporciones del cuerpo humano como en las ramas de los árboles.
En
realidad, en la naturaleza no sólo es posible encontrar la sección áurea,
sino casi cualquier otra norma proporcional que uno se proponga: todo depende de
las partes que uno elija para medir.
El
rol de Lucca Pacioli fue el de legitimador de una norma proveniente del mundo de
los negocios, máximo valor social del Renacimiento. Si hoy continuamos legitimándola,
lo que estamos haciendo, aunque sin tener conciencia de ello, es poner de
manifiesto que lo que verdaderamente nos importa es tener claro cómo nos
repartimos el mundo.
En
matemáticas, una proporción de la geometría que se obtiene al dividir un
segmento en dos partes de manera que el cociente entre la longitud del segmento
mayor y la longitud del segmento inicial es igual al cociente entre la longitud
del segmento menor y la del segmento mayor.
![]()
El
punto C crea una sección áurea en el
segmento rectilíneo AB si AC/AB = CB/AC.
Esta proporción tiene el valor numérico 0,618..., que se puede calcular de la
siguiente manera: si AB = 1 y la
longitud de AC = x,
entonces AC/AB = CB/AC se convierte en x/1
= (1 - x)/x. Multiplicando ambos lados de esta ecuación por x,
se tiene que x2
= 1 - x; y por tanto x2
+ x - 1 = 0. Esta ecuación de segundo
grado se puede resolver utilizando la fórmula cuadrática, que da x
= (-1 + Ä)/2 = 0,6180339...
Ciertos
historiadores afirman que las propiedades de las secciones áureas ayudaron a
los discípulos del matemático y filósofo griego Pitágoras a descubrir las rectas
inconmensurables, que son el equivalente geométrico de los números
irracionales. Sin embargo, lo que sí es cierto es que desde la antigüedad,
muchos filósofos, artistas y matemáticos se han interesado por la sección áurea,
que los escritores del renacimiento llamaron proporción
divina.
Los sistemas matemáticos de proporcionalidad surgidos del concepto pitagórico de que “todo es número” y de la creencia de que ciertas relaciones numéricas reflejan la estructura armónica del universo. Una de estas relaciones, en vigencia desde la Antigüedad hasta nuestros días, es la proporción conocida como la sección áurea, los griegos ya descubrieron su importante cometido en la proporción del cuerpo humano. Al creer que el hombre y los templos debían pertenecer a un orden universal más elevado, en la misma estructura de los templo se ponían de manifiesto estas proporciones.

Este
dibujo, titulado Las proporciones del hombre, procede de un cuaderno de apuntes de
Leonardo da Vinci. Está basado en las teorías del arquitecto romano Marco
Vitrubio sobre la aplicación de la sección áurea al ser humano: la proporción
entre la distancia desde la cabeza hasta el ombligo y desde éste hasta los
pies, debe ser la misma que la proporción entre la distancia desde el ombligo
hasta los pies y desde la cabeza hasta los pies. El hecho de que este sistema de
relaciones armónicas, también conocido como la proporción divina, pudiera
trasladarse a la figura humana, tuvo una gran importancia durante el
renacimiento.
La
sección áurea mereció, también, la atención de los arquitectos de
Renacimiento. En tiempos más recientes, Le
Corbusier basó su sistema Modular en la sección áurea y su aplicación
en la arquitectura perdura hoy en día,
se rige por las medidas de una figura humana erguida con el brazo levantado. El
autor creó dos escalas para las estaturas de 1,75 y 1,83 metros,
respectivamente. El sistema se aplica para el dimensionamiento de habitaciones.
COSTRUCCIÓN
GEOMÉTRICA DE LA SECCIÓN ÁUREA
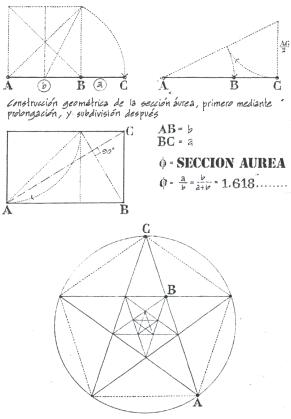
Los sistemas matemáticos de
proporcionalidad surgidos del concepto pitagórico de que "todo es
numero" y de la creencia de que ciertas relaciones numéricas reflejan la
estructura armónica del universo.
Una
de estas relaciones, en vigencia desde la antigüedad hasta nuestros días, es
la proporción conocida como la sección áurea, los griegos ya descubrieron su
importante cometido en la proporción del cuerpo humano.
Al
creer que los hombres y los templos debían pertenecer a un orden universal más
elevado, en la misma estructura de los templos se ponían de manifiesto estas
proporciones. La relación áurea mereció, también la atención de los
arquitectos del renacimiento. En tiempos más recientes Le Cobusier baso su
sistema modulor en la sección áurea, y su aplicación en la arquitectura
perdura hoy en día.
La
sección áurea se puede definir geométricamente como un segmento rectilíneo
dividido de manera que la parte menor es a la mayor como esta lo es al total.
Algebraicamente se expresa mediante
una ecuación de dos razones: a/b = b/a+b.
Las
propiedades de que goza explicar su presencia en la arquitectura y en la
estructura de los organismos vivos. Cualquier progresión que se base en la
sección áurea será el, al mismo tiempo aritmética y geometría.
1
2 3
n
En la progresión numérica: 1, 0, 0, 0,...,0 , cada elemento es la suma de los dos anteriores. Otra serie que se aproxima a la áurea es la serie numérica de Fibonacci : 1, 1, 2, 3, 5, 8, 13,..., etc. De nuevo cada número es igual a la suma de los dos que le anteceden y la razón entre dos términos consecutivos tiende a acercarse a la sección áurea conforme progresa la serie.
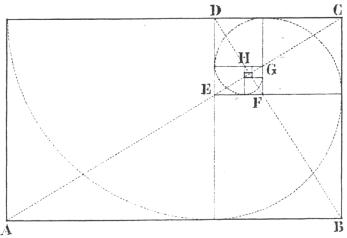
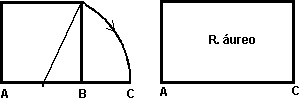
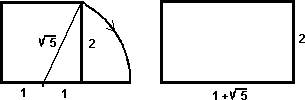
Un
rectángulo cuyos lados se han proporcionados de acuerdo a la sección áurea se
denomina rectángulo áureo. Si sobre su lado menor se construye un cuadrado, la
superficie restante será menor, pero será también un rectángulo análogo al
primero. Esta operación puede repetirse hasta el infinito y crear una gradación
de cuadrados y de rectángulos áureos. Durante esta transformación cada un a
de las partes sigue siendo análoga a las restantes y al todo.